  


Because Mathematics can be so fun!
K3DSurf is a program to visualize and manipulate Mathematical models in three, four, five and six dimensions.
K3DSurf supports Parametric equations and Isosurfaces.

Because an image is worth 1000 words... (*)




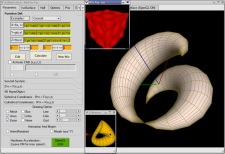
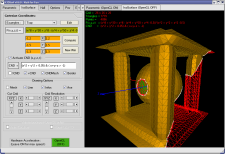
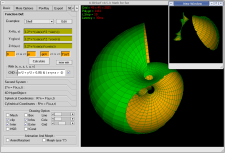



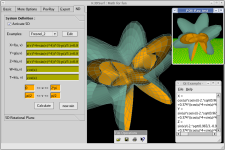
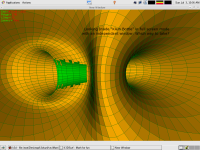
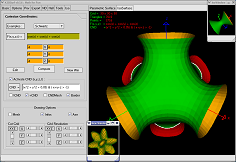
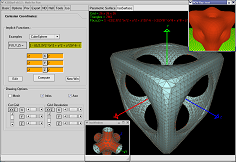


And because (*) isn't totally true...
Features
Studying mathematical surfaces with K3DSurf include doing:
-
Interactive visualization with mouse events (Right: Rotate, Middle: translate
and left: Scale).
-
Real time animation (rotation) and morph (by the introduction of t_time variable). Animation and morph
can also be monitored by controls that affect the CPU usage and t_time step.
-
Creat screenshots by copying the draw window or by using the best ray tracer on the net: Povray.
Creat movie scene is also supported
-
Generat Mesh files that describe the shape of the mathematical model.
Supported formats are:
-
Povscript : Povray is the best ray tracer available on the net...and it's free.
-
VRML2: to use with the majority of current browsers via an appropriate plug-in.
-
OBJ: a well-known file format supported by the majority of 3D applications (Blender, MAYA and Moray...).
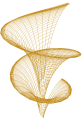
K3DSurf Usage
K3DSurf can be used by every one interested in 3D Mathematical drawing functions and don't require any
special competences by users. Most of the work was done with the intention to make K3DSurf as simple
as possible but without any harm of it's efficiency:
-
K3DSurf program is developed for being used by beginner users with low level degree in Mathematical science
simply by testing examples (more than 50) given with it and by rendering them with Povray.
Add/remove some functions from equations and visualize new results is the best way to understand
3D mathematical functions behaviours.
-
2D and 3D Designers: Pov scripts (and other file formats) generated by
K3DSurf can also be integrated in complicated scenes. Adding textures to mesh
objects under Povray, for examples, is straightforward.
-
Teachers and height level students can study very complicated
surfaces with K3DSurf. 4D/5D hyperobjects is another field where talented competences
can give their best to discover new entity with artefacts that are not obvious to
understand for a neophyte.
Creating equations to represent specific shapes can be somewhat tricky and require
experiences in both Mathematic field and 3D programing but the most "experience demanding", I think, is
the creation of specific equations with specific behaviors when rotating in Hyperspace (4D/5D).

K3DSurf Overview
Parametric Surface/curve :
K3DSurf use parametric descriptions of it's physical models.
The parametric method of representing surfaces/curves uses a function
to map some portion of R2 (the domain) to a patch of the surface in R3.
Because any position in the plane, and thus any position on the surface
patch, can be uniquely given by two coordinates, the surface is said to
be parameterized by those coordinates.
Parametric equations can be either “Implicit” or “Explicit”:
** Explicit equations:
In an explicit equations, x, y, and z are each given by separate
functions of parameters u and v.
Example: X =u, Y = u+v, Z = cos(u+v)
** Implicit equations: Right now, only implicit equations like Z^n =
f(X,Y) with (n mod 2 = 1) are supported by K3DSurf.
Example: Z = exp(x^2 + y^2), Z^7 = exp(x*cos(y))...

K3DSurf defined functions:
K3DSurf support all functions listed here :
| Function |
Symbol |
| Sine |
sin() |
| Cosine |
cos() |
| Tangent |
tan() |
| Arc Sine |
asin() |
| Arc Cosine |
acos() |
| Arc Tangent |
atan() |
| Hyperbolic Sine |
sinh() |
| Hyperbolic Cosine |
cosh() |
| Hyperbolic Tangent |
tanh() |
| Inverse Hyperbolic Sine |
asinh() |
| Inverse Hyperbolic Cosine |
acosh() |
| Inverse Hyperbolic Tangent |
atanh() |
| Natural Logarithm |
log() |
| Logarithm base 10 |
log10() |
| Angle |
angle() |
| Absolute Value / Magnitude |
abs() |
| Secant (equivalent to 1/cos()). |
sec() |
| Cscant (equivalent to 1/sin()). |
csc() |
| Cotant (equivalent to 1/tan()). |
cot() |
| Modulus |
mod() |
| Square Root |
sqrt() |
| Exponential |
exp() |
| Min(A,B) |
min(A,B) |
| Max(A,B) |
max(A,B) |
| Rounds to the closest integer |
int() |
| Constants |
pi |

User defined functions :
You can define your own function by using «Function definition" area in "More Option" page.
Exemple :
k(u,v,t,x,y) = sin(u)*cos(v)*t*x
X = u
Y = cos(v)*k(u,v,t,x,y) <-- cos(v)*[sin(u)*cos(v)*t*x]
Z = cos(u)
You can also use the function "k" for more complicated purpose like:
X = u
Y = v
Z = k(exp(u)*t,u,v,t,t) <-- sin(exp(u)*t)*cos(u)*v*t
NB: The definition of the function k use (u,v,t,x,y) parameters which are
different compared to (u,v,t,x,y) used in parametric equations.

Animation and Morph :
** Animation consists in 3D rotation of the object.
Direction and speed of the rotation are controlled with Mouse Button direction and speed.
** Morph consists on the introduction of new parameter “t” inside parametric
equations.
Example:
X = u
Y = v
Z = sin(pi*((u)^2+(v)^2))/2 ==> sin(t*pi*((u)^2+(v)^2))/2
You have to click « calculate » button to register the new equation.
Now, activate Morph effect (basic-->AimationAndMorph-->Morph).
You can also combine Animation and Morph effects. In addition, you can control
CPU usage and t_step in “More Option” page.
Forum :
To discussu about K3DSurf : http://k3dsurf.s4.bizhat.com/
Download :
Download K3DSurf For :



For More Download :
kde-apps.org : http://kde-apps.org/content/show.php?content=25049
Please don't forget to give your VOTE good/bad (No need to be registred to do this)
Or
SourceForge.net : http://sourceforge.net/project/showfiles.php?group_id=142839
Contact :
Developer : Abderrahman Taha (taha_ab@yahoo.fr)
Specific Package Maintainer(s) :
Those peoples are kindly building packages for you. Contact them directly
for wishes/suggestions about theirs efforts:
Linux :
Debian package -->Cyril Brulebois (Official Debian)
(email,
link )
RPM package -->
Dries Verachtert (email,
link )
MacOSX :
François Le Coat (email,
link )
FreeBSD :
Thierry Thomas (email,
link )
Windows :
Me (email)
My Favorite Links :
3D Graphic Infos --> Linuxgraphic(http://www.linuxgraphic.org/)
Development Environment --> KDevelop(http://www.kdevelop.org/)
Free Science Tools--> freescience(http://www.freescience.info)
Scientific Questions --> Science Forums(http://www.scienceforums.com)
This WebSite is hosted under SourceForge.net :
The world's largest development and download
repository of Open Source code and applications
|

|
|






























