  


parce que les mathématiques peuvent être un vrai plaisir!
K3DSurf est un programme qui permet la visualisation et la manipulation de modèles
mathématiques dans
l'espace de trois, quatre, cinq et six dimensions. K3DSurf supporte les équations Paramétriques et les Isosurfaces.

Parce qu'une image vaut 1000 mots... (*)




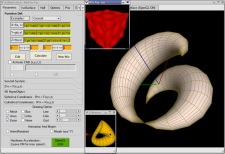
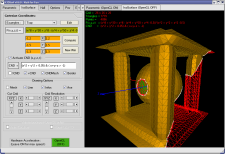
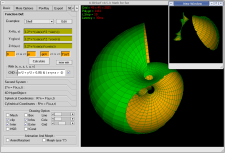



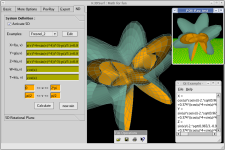
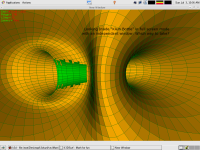
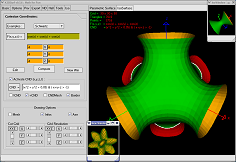
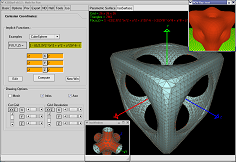


Et parce que (*) n'est pas totalement vraie...
Fonctionnalités :
L'étude des surfaces mathématiques avec K3DSurf inclut la possibilité de faire :
-
Visualisation interactive avec les événements souris(Droit: Rotation, Milieu: Translation
et Gauche: Agrandissement).
-
Animation en temps réel(rotation) et morphe (avec l'introduction d'une nouvelle variable t_temps).
L'animation et l'effet morphe peuvent aussi être asservis par des contrôles qui affectent la CPU et
le pas t_temps.
-
Créer des prises d'écrans par copiage de la fenêtre de dessin ou par l'utilisation du meilleur lance de rayon
sur la toile : Povray.
La création de séquences animées est aussi possible.
-
Générer des fichiers Mesh qui décrivent la forme du modèle mathématique
les formats de fichiers supportés sont :
-
Povscript : Povray est le meilleur Raytracer disponible sur la toile...et il est gratuit.
-
VRML2: A utiliser avec la majorité des fureteurs actuels a travers un module approprié.
-
OBJ: Un format très bien supporté par la majorité des applications 3D (Blender, MAYA et Moray).
Utilisation de K3DSurf
K3DSurf peut être utilisé par toute personne intéressée par le dessin des fonctions
mathématiques 3D et
ne requiert pas de compétences spéciales par les utilisateurs. Une grande partie du travail a
été faite
avec l'intention de rendre l'utilisation de K3DSurf la plus simple possible mais sans
altération de son efficacité:
-
K3DSurf est un programme développé pour être utilisé par des utilisateurs au niveau
mathématique peu élevé simplement par test des exemples (plus de 50) qui viennent avec
d'office et par utilisation de Povray pour les dessiner.
L'ajout/Retrait de quelques fonctions des équations et la visualisation du nouveau
résultat est la meilleure façon pour appréhender le comportement des fonctions mathématiques
-
Architectes 2D/3D : Les scripts Pov (et autres formats de fichiers) génèrés par K3DSurf peuvent aussi
être intégrés dans des scènes plus complexes. L'ajout de textures aux Objets Mesh sous Povray, par
exemple, est une opération très simple.
-
Les Enseignants et étudiants de haut niveau peuvent étudier des surfaces très complexes avec k3DSurf.
les HyperObjets 4D/5D est un autre domaine ou des personnes compétentes en la matière peuvent
donner leur meilleur pour la découverte de nouvelles entités avec des artefacts qui ne sont pas
évidents à découvrir ou à comprendre par des néophytes.

Survol de K3DSurf
Surface/courbe paramétriques :
K3DSurf utilise une description paramétrique de ses modèles mathématiques.
La méthode paramétrique pour représenter une surface/courbe utilise une fonction
pour calquer des portions de R2 (le domaine) sur une partie de la surface dans R3.
parce que n'importe quelle position dans R2, et ainsi n'importe quelle position dans
R3, peut être décrite par deux coordonnées, la surface est dite "paramétrable"
par ces deux coordonnées.
Les équations paramétriques peuvent être soit "Implicites" soit "Explicites":
** Équations Explicites:
Dans une équation explicite, les coordonnées x, y et z sont toutes fonctions
des paramètres u et v.
Exemple: X =u, Y = u+v, Z = cos(u+v)
** Équations Implicites: Pour le moment, seules les équations de la forme Z^n =
f(X,Y) avec (n mod 2 = 1) sont supportées par K3DSurf.
Exemple: Z = exp.(x^2 + y^2), Z^7 = exp.(x*cos(y))...

Les fonctions définies de K3DSurf:
K3DSurf supporte toutes les fonctions définies dans la liste en bas:
| Function |
Symbol |
| Sine |
sin() |
| Cosine |
cos() |
| Tangent |
tan() |
| Arc Sine |
asin() |
| Arc Cosine |
acos() |
| Arc Tangent |
atan() |
| Hyperbolic Sine |
sinh() |
| Hyperbolic Cosine |
cosh() |
| Hyperbolic Tangent |
tanh() |
| Inverse Hyperbolic Sine |
asinh() |
| Inverse Hyperbolic Cosine |
acosh() |
| Inverse Hyperbolic Tangent |
atanh() |
| Natural Logarithm |
log() |
| Logarithm base 10 |
log10() |
| Angle |
angle() |
| Absolute Value / Magnitude |
abs() |
| Secant (equivalent to 1/cos()). |
sec() |
| Cscant (equivalent to 1/sin()). |
csc() |
| Cotant (equivalent to 1/tan()). |
cot() |
| Modulus |
mod() |
| Square Root |
sqrt() |
| Exponential |
exp() |
| Min(A,B) |
min(A,B) |
| Max(A,B) |
max(A,B) |
| Rounds to the closest integer |
int() |
| Constants |
pi |

Fonctions définies par les utilisateurs:
Vous pouvez définir vos propres fonctions par l'utilisation de «Function definition»
dans la page "More Option".
Exemple :
k(u,v,t,x,y) = sin(u)*cos(v)*t*x
X = u
Y = cos(v)*k(u,v,t,x,y) <-- cos(v)*[sin(u)*cos(v)*t*x]
Z = cos(u)
Vous pourrez utiliser la fonction "k" de façon plus compliquées comme dans:
X = u
Y = v
Z = k(exp(u)*t,u,v,t,t) <-- sin(exp(u)*t)*cos(u)*v*t
NB: La définition de la fonction «k» utilise les paramètres (u,v,t,x,y) qui ont une
signification différente des paramètres (u,v,t,x,y) utilisés dans les équations paramétriques.

Animation et Morph :
** Animation consiste dans la rotation 3D de l'Objet.
la direction et la vitesse de rotation peuvent être contrôlées par la vitesse et la direction
de la souris.
** Morph consiste en l'introduction d'un nouveau paramétre «t» dans les équations paramétriques.
Example:
X = u
Y = v
Z = sin(pi*((u)^2+(v)^2))/2 ==> sin(t*pi*((u)^2+(v)^2))/2
Vous devez cliquer sur le boutton "calculate" pour enregistrer les nouvelles équations.
maintenant, activer l'effet Morph avec (basic-->AimationAndMorph-->Morph).
Vous pourrez aussi combiner l'effet Aimation et Morph. En plus, le contrôle de l'utilisation
CPU et le pas t_temps est possible a partir de la page “More Option”.
Forum :
Pour discuter sur K3DSurf : http://k3dsurf.s4.bizhat.com/
Téléchargement:
télécharge K3DSurf Pour :



Pour plus de téléchargement :
S.V.P n'oubliez pas de VOTER sur le site de kde-apps
(pas besoin de s'inscrire)
kde-apps.org : http://kde-apps.org/content/show.php?content=25049
Ou
SourceForge.net : http://sourceforge.net/project/showfiles.php?group_id=142839
Contact :
Développeur : Abderrahman Taha (taha_ab@yahoo.fr)
Maintainer(s) :
Linux :
Debian package -->Cyril Brulebois (Debian Officielle)
(email,
link )
RPM package -->
Dries Verachtert (email,
link )
MacOSX :
Mac package -->
François Le Coat (email,
link )
FreeBSD :
Thierry Thomas (email,
link )
Windows :
Moi (email)
Liens :
Infos 3D --> Linuxgraphic(http://www.linuxgraphic.org/)
développement --> KDevelop(http://www.kdevelop.org/)
Outils scientifiques gratuits --> freescience(http://www.freescience.info)
Questions Scientifiques --> Science Forums(http://www.scienceforums.com)
This WebSite is hosted under SourceForge.net :
The world's largest développement and download
repository of Open Source code and applications
|

|
|






























